H7-Unit_4-Policy_Gradient_with_PyTorch-D3-gradient

中英文对照学习，效果更佳！
原课程链接：https://huggingface.co/deep-rl-course/unit8/clipped-surrogate-objective?fw=pt

Diving deeper into policy-gradient methods

更深入地研究政策梯度方法

Getting the big picture

了解大局

We just learned that policy-gradient methods aim to find parameters θ \theta θ that maximize the expected return.

我们刚刚了解到，政策梯度方法的目标是找到使预期收益最大化的参数θ\thetaθ。

The idea is that we have a parameterized stochastic policy. In our case, a neural network outputs a probability distribution over actions. The probability of taking each action is also called action preference.

我们的想法是，我们有一个参数化的随机策略。在我们的例子中，神经网络输出动作的概率分布。采取每一种行动的概率也称为行动偏好。

If we take the example of CartPole-v1:

如果我们以CartPole-v1为例：

• As input, we have a state.
• As output, we have a probability distribution over actions at that state.

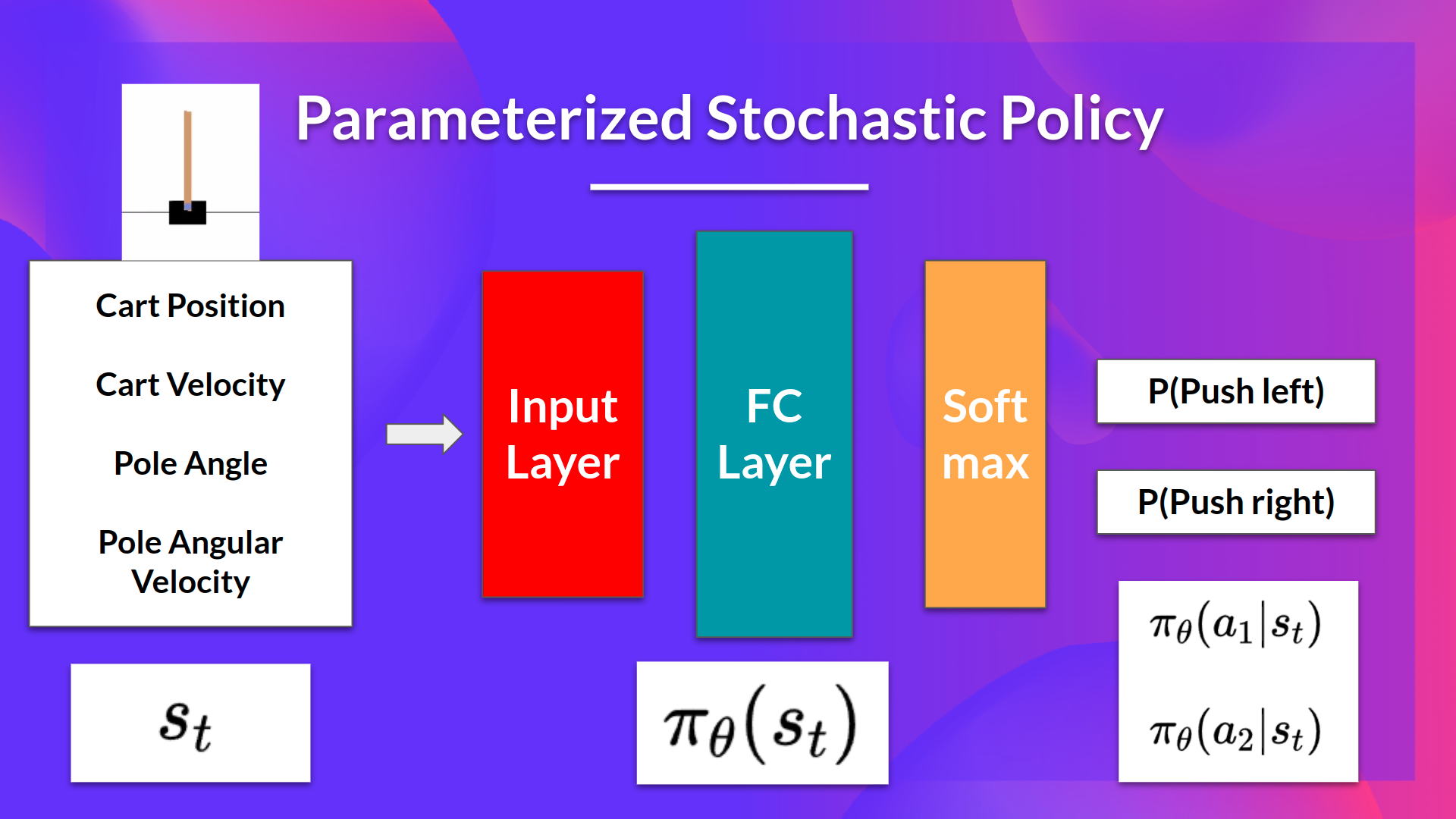
Our goal with policy-gradient is to control the probability distribution of actions by tuning the policy such that good actions (that maximize the return) are sampled more frequently in the future.
Each time the agent interacts with the environment, we tweak the parameters such that good actions will be sampled more likely in the future.

作为输入，我们有一个状态。作为输出，我们有一个关于该状态下动作的概率分布。基于策略的我们的目标是通过调整策略来控制动作的概率分布，以便在未来更频繁地采样好的动作(最大化回报)。每次代理与环境交互时，我们都会调整参数，以便在未来更有可能采样到好的操作。

But how are we going to optimize the weights using the expected return?

但是，我们如何使用预期收益来优化权重呢？

The idea is that we’re going to let the agent interact during an episode. And if we win the episode, we consider that each action taken was good and must be more sampled in the future
since they lead to win.

我们的想法是让特工在一集中进行互动。如果我们赢得了这一集，我们认为所采取的每一项行动都是好的，而且必须在未来进行更多的采样，因为它们导致了胜利。

So for each state-action pair, we want to increase the P(a∣s)P(a|s)P(a∣s): the probability of taking that action at that state. Or decrease if we lost.

所以对于每个状态-动作对，我们想要增加P(a∣s)P(a|s)P(a∣s)：在该状态下采取该动作的概率。或者如果我们输了就会减少。

The Policy-gradient algorithm (simplified) looks like this:

策略梯度算法(简化)如下所示：

Now that we got the big picture, let’s dive deeper into policy-gradient methods.

政策梯度大局现在我们已经了解了大局，让我们更深入地研究政策梯度方法。

Diving deeper into policy-gradient methods

更深入地研究政策梯度方法

We have our stochastic policy π\piπ which has a parameter θ\thetaθ. This π\piπ, given a state, outputs a probability distribution of actions.

我们有我们的随机策略π\piπ，它有一个参数θ\θ。该π\piπ在给定状态的情况下输出动作的概率分布。

Where πθ(at∣st)\pi_\theta(a_t|s_t)πθ​(at​∣st​) is the probability of the agent selecting action ata_tat​ from state sts_tst​ given our policy.

策略，其中∣(at∣st)\pi_\theta(a_t|s_t)​(at​∣st​)是代理在给定策略的情况下从状态sts_tst​中选择操作ata_tat​的概率。

But how do we know if our policy is good? We need to have a way to measure it. To know that, we define a score/objective function called J(θ)J(\theta)J(θ).

但是我们怎么知道我们的政策是不是好呢？我们需要有一种方法来衡量它。为了了解这一点，我们定义了一个分数/目标函数J(θ)J(\theta)J(θ)。

The objective function

目标函数

The objective function gives us the performance of the agent given a trajectory (state action sequence without considering reward (contrary to an episode)), and it outputs the expected cumulative reward.

目标函数给出了给定的轨迹(不考虑奖励的状态动作序列(与情节相反))代理的表现，并输出了预期的累积奖励。

Let’s detail a little bit more this formula:

Return让我们更详细地了解此公式：

• The expected return (also called expected cumulative reward), is the weighted average (where the weights are given by P(τ;θ)P(\tau;\theta)P(τ;θ) of all possible values that the return R(τ)R(\tau)R(τ) can take.

预期收益(也称为预期累积回报)是收益R(τ；θ)R(\tau)R(\tau)R(τ；θ)可取的所有可能值的加权平均值(其中权重由P(τ)P(\tau；\theta)P(τ)给出。

• R(τ)R(\tau)R(τ) : Return from an arbitrary trajectory. To take this quantity and use it to calculate the expected return, we need to multiply it by the probability of each possible trajectory.
• P(τ;θ)P(\tau;\theta)P(τ;θ) : Probability of each possible trajectory τ\tauτ (that probability depends on θ \thetaθ since it defines the policy that it uses to select the actions of the trajectory which as an impact of the states visited).

R(τ)R(\tau)R(τ)：从任意轨迹返回。为了获得这个数量并使用它来计算预期收益，我们需要将它乘以每个可能轨迹的概率。P(τ；θ)P(\tau；\theta)P(τ；θ)：每个可能轨迹的概率τ\tauτ(该概率取决于θ\thetaθ，因为它定义了用于选择轨迹的动作作为所访问状态的影响的策略)。概率

• J(θ)J(\theta)J(θ) : Expected return, we calculate it by summing for all trajectories, the probability of taking that trajectory given θ\theta θ, and the return of this trajectory.

Our objective then is to maximize the expected cumulative reward by finding θ\theta θ that will output the best action probability distributions:

J(θ)J(\theta)J(θ)：预期回报，我们通过对所有轨迹求和，在给定θ\thetaθ的情况下采用该轨迹的概率，以及该轨迹的返回来计算预期回报。然后，我们的目标是通过找到将输出最佳行动概率分布的θ\thetaθ来最大化预期累积回报：

最高目标

Gradient Ascent and the Policy-gradient Theorem

梯度上升与政策梯度定理

Policy-gradient is an optimization problem: we want to find the values of θ\thetaθ that maximize our objective function J(θ)J(\theta)J(θ), we need to use gradient-ascent. It’s the inverse of gradient-descent since it gives the direction of the steepest increase of J(θ)J(\theta)J(θ).

政策梯度是一个优化问题：我们要找到θ\thetaθ的值，使我们的目标函数J(θ)J(\theta)J(θ)最大化，我们需要使用梯度上升法。这是与梯度下降相反的，因为它给出了J(θ)J(\theta)J(θ)最陡峭增长的方向。

(If you need a refresher on the difference between gradient descent and gradient ascent check this and this).

(如果你需要复习一下渐变下降和渐变上升之间的区别，请检查这个和这个)。

Our update step for gradient-ascent is:

我们对梯度上升的更新步骤是：

θ←θ+α∗∇θJ(θ) \theta \leftarrow \theta + \alpha * \nabla_\theta J(\theta) θ←θ+α∗∇θ​J(θ)

←∗∇←∗∇​J(θθ+αθJ(θ)\θθ+αθLeftarrow J(θ))

We can repeatedly apply this update state in the hope that θ\theta θ converges to the value that maximizes J(θ)J(\theta)J(θ).

我们可以重复应用这种更新状态，希望θ\thetaθ收敛到使J(θ)J(\theta)J(θ)最大化的值。

However, we have two problems to obtain the derivative of J(θ)J(\theta)J(θ):

然而，我们有两个问题来获得J(θ)J(\theta)J(θ)的导数：

1. We can’t calculate the true gradient of the objective function since it would imply calculating the probability of each possible trajectory which is computationally super expensive.
   We want then to calculate a gradient estimation with a sample-based estimate (collect some trajectories).
2. We have another problem that I detail in the next optional section. To differentiate this objective function, we need to differentiate the state distribution, called Markov Decision Process dynamics. This is attached to the environment. It gives us the probability of the environment going into the next state, given the current state and the action taken by the agent. The problem is that we can’t differentiate it because we might not know about it.

Fortunately we’re going to use a solution called the Policy Gradient Theorem that will help us to reformulate the objective function into a differentiable function that does not involve the differentiation of the state distribution.

我们不能计算目标函数的真实梯度，因为这意味着要计算每个可能轨迹的概率，这在计算上是非常昂贵的。然后，我们希望使用基于样本的估计来计算梯度估计(收集一些轨迹)。我们还有另一个问题，我将在下一个可选部分详细说明。为了区分这个目标函数，我们需要区分状态分布，称为马尔可夫决策过程动力学。这与环境息息相关。它为我们提供了环境进入下一状态的可能性，给定了当前状态和代理所采取的操作。问题是我们不能区分它，因为我们可能不知道它。幸运的是，我们将使用一种名为政策梯度定理的解决方案，它将帮助我们将目标函数重新表述为可微函数，而不涉及状态分布的微分。

If you want to understand how we derivate this formula that we will use to approximate the gradient, check the next (optional) section.

政策梯度如果你想了解我们是如何推导出这个公式的，我们将使用它来近似梯度，请查看下一节(可选)。

The Reinforce algorithm (Monte Carlo Reinforce)

增强算法(蒙特卡罗增强)

The Reinforce algorithm, also called Monte-Carlo policy-gradient, is a policy-gradient algorithm that uses an estimated return from an entire episode to update the policy parameter θ\thetaθ:

强化算法也称为蒙特卡罗策略梯度，是一种策略梯度算法，它使用整个剧集的估计回报来更新策略参数θ\thetaθ：

In a loop:

在循环中：

• Use the policy πθ\pi_\thetaπθ​ to collect an episode τ\tauτ
• Use the episode to estimate the gradient g^=∇θJ(θ)\hat{g} = \nabla_\theta J(\theta)g^​=∇θ​J(θ)

使用策略​∇πθ\pi_\thetaπθττ​估计梯度g^=∇​J(πθ)\θ{g}=\nabla_\theta J(\theta)g^τ=θJ(θ)策略梯度

• Update the weights of the policy: θ←θ+αg^\theta \leftarrow \theta + \alpha \hat{g}θ←θ+αg^​

The interpretation we can make is this one:

更新策略的权重：←←​g^\θθ+αg^\theta\θθ+α\theta+\Alpha\Hat{g}Leftarrow我们可以做出这样的解释：

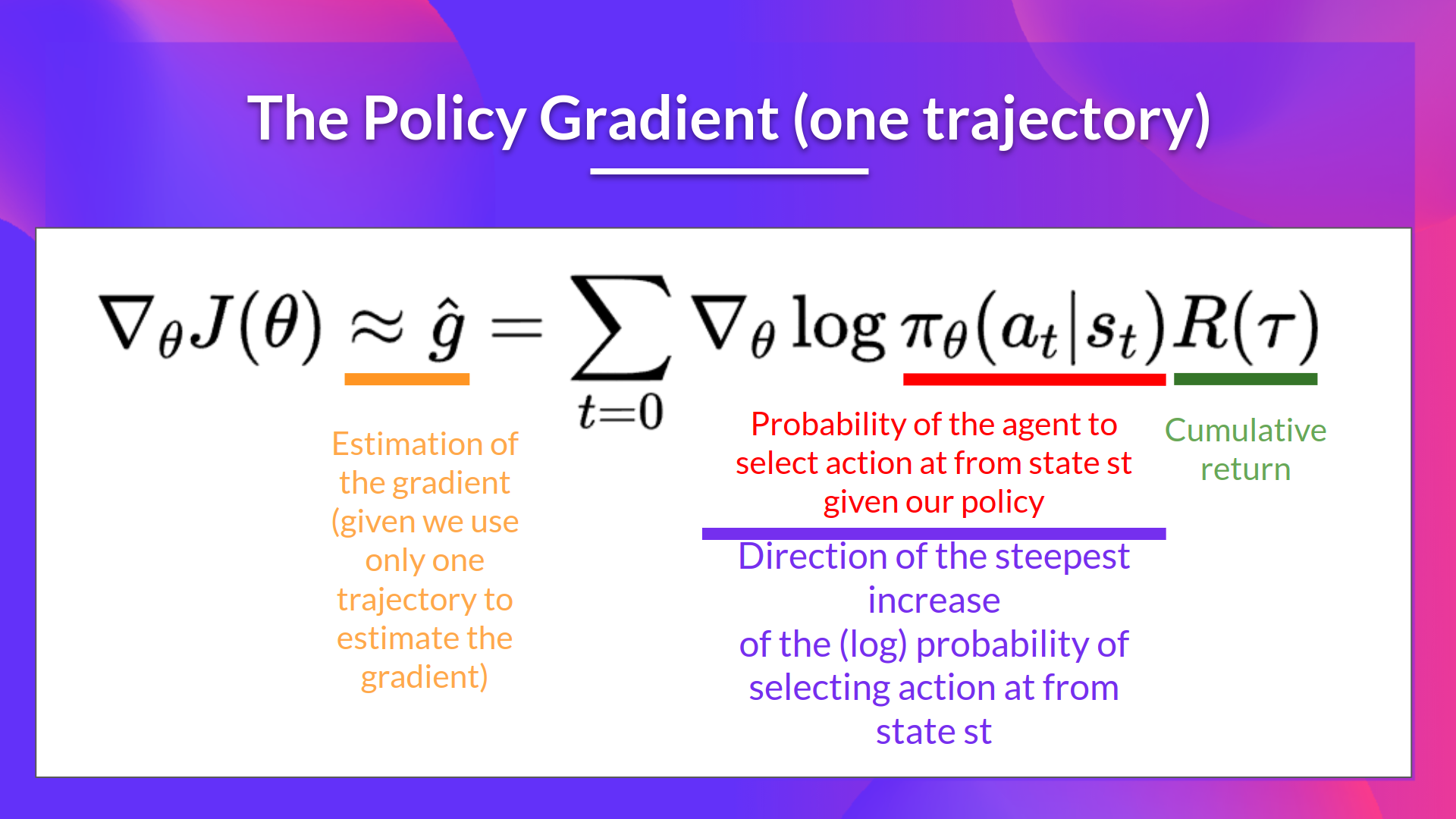
• ∇θlogπθ(at∣st)\nabla_\theta log \pi_\theta(a_t|s_t)∇θ​logπθ​(at​∣st​) is the direction of steepest increase of the (log) probability of selecting action at from state st.
  This tells us how we should change the weights of policy if we want to increase/decrease the log probability of selecting action ata_tat​ at state sts_tst​.
• R(τ)R(\tau)R(τ): is the scoring function:
  • If the return is high, it will push up the probabilities of the (state, action) combinations.
  • Else, if the return is low, it will push down the probabilities of the (state, action) combinations.

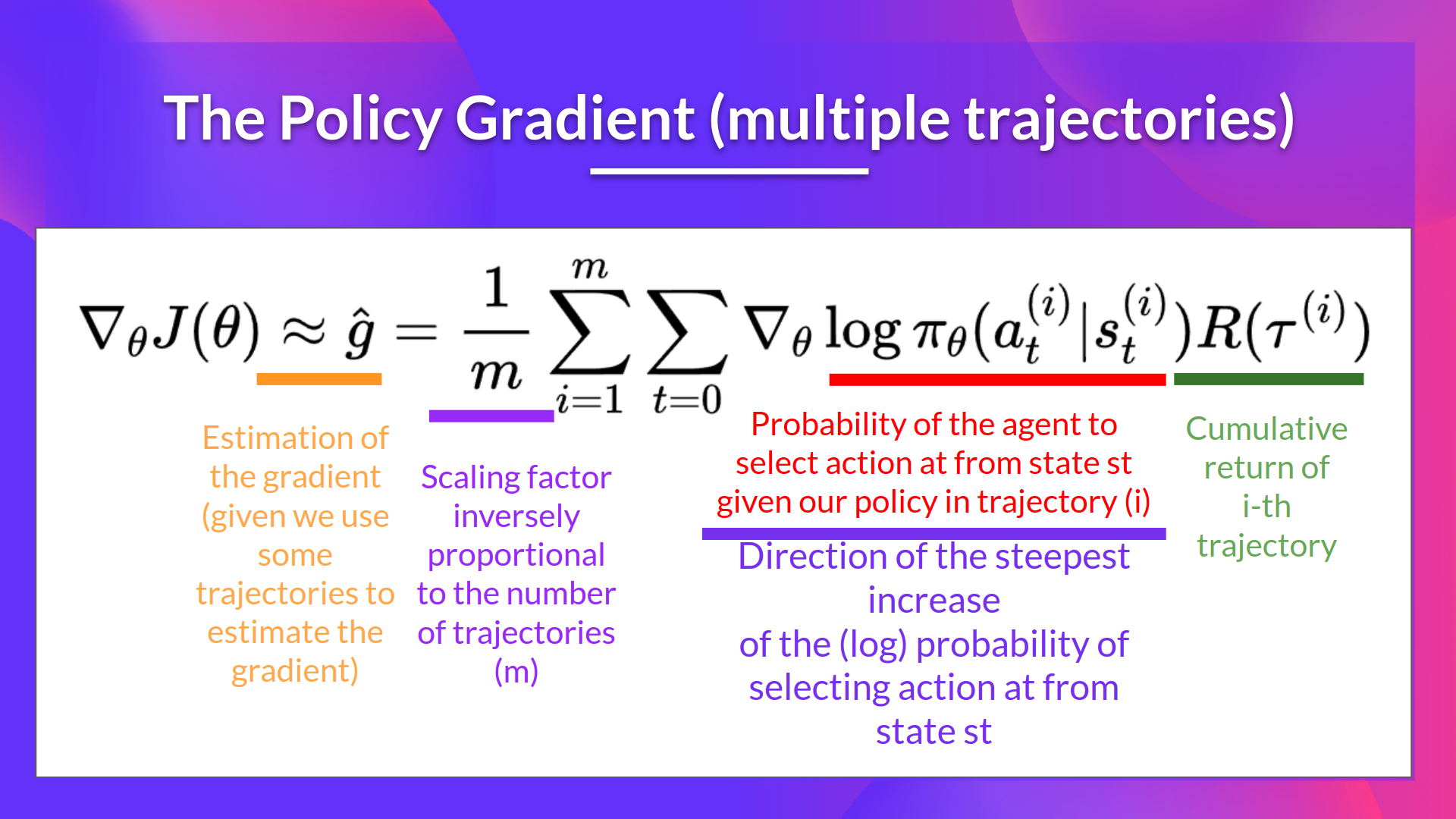
We can also collect multiple episodes (trajectories) to estimate the gradient:

∇Log Log(at∣st)\nabla_\theta Log\pi_\theta(a_t|s_t)∇​​(at​∣st​)是从状态st选择动作at的概率(θπθθπθ)最陡峭增加的方向。这告诉我们，如果我们想要增加/减少​在STS_TST​状态下选择动作ATA_TAT的对数概率，我们应该如何改变策略的权重。R(τ)R(\tau)R(τ)：是计分函数：如果收益率高，它将推高(状态，动作)组合的概率。此外，如果收益率低，它将推低(状态，动作)组合的概率。我们还可以收集多个情节(轨迹)来估计梯度：

政策梯度